数学が伸び悩んでいる、あるいは数学的なセンスに自信を持てない人が運や直観力に頼ることなく安定的に合格水準の得点ができるようになるにはどうすればよいのでしょうか。理系は言わずもがな一定の数学力が要求されるでしょう。数学が苦手な文系でも数学の成績が他教科の足を引っ張るのは避けたいし、逆に数学の得点率が高まると大きなアドバンテージになるはずです。
この記事では高校数学の理解の基礎となる、命題、条件、同値変形といった事項を身に着け、凡人が凡人なりに数学の成績を伸ばす方法について考えてみます。
自分の理解に何が足りていないのか?
問題集を3周する、といったように分からない問題を身につくまで繰り返し解く勉強法がアドバイスとしてあります。しかし、筆者もそうでしたが、分からない問題を暗記物として繰り返し練習したとしてもすぐに忘れるうえ類題も解けるようにならず、苦しさを覚えて挫折してしまう人がいるのではないでしょうか。そういった人は自分が何が分からないのかも分からず、数学の得点が上がらないのは自分の練習量が不足しているのだ、と思う傾向があります。
そのような悪循環の裏で、複雑で難しく見える問題が実際にはそれほど難しくないことを組み合わせているにすぎないということがあります。すなわち、思っているよりもずっとシンプルな理解の仕方が可能であることに気づかない場合があるのです。しかしながら、普通に売られている参考書では丁寧な解説を売りにしているものも含めて、答案の中で「一体何をやっているのか」、「なぜそれをする必要があるのか」といったことを把握するのはかなり難しく、コツを要します。数学ができる人の脳内はよくわかりませんが、彼らはこういった点を把握しつつ、数学ができない人よりももっとシンプルな理解ができているのではないかと思います。
複数の問題に通底する、より大きな枠組みが存在するのにも関わらずそれぞれを別々の問題として捉えてしまう。「より大きな枠組み」、と言いましたが実際それを掴むためにはどうすればよいのでしょうか。
そういった枠組みの把握のために大きなカギを握るのは論理であると自分は考えます。必然性を支えるのが論理であり、基礎の基礎ではあるのですが、あまり重点的に説明される機会がありません。論理を改めて学ぶことで、答案の構造(=骨組み)や仕組みを幾分かクリアにすることができるのです。数学ができない人ほど論理について学ぶ必要があり、決して無駄にはならないはずです。
論理について勉強することが、どのように役立つか
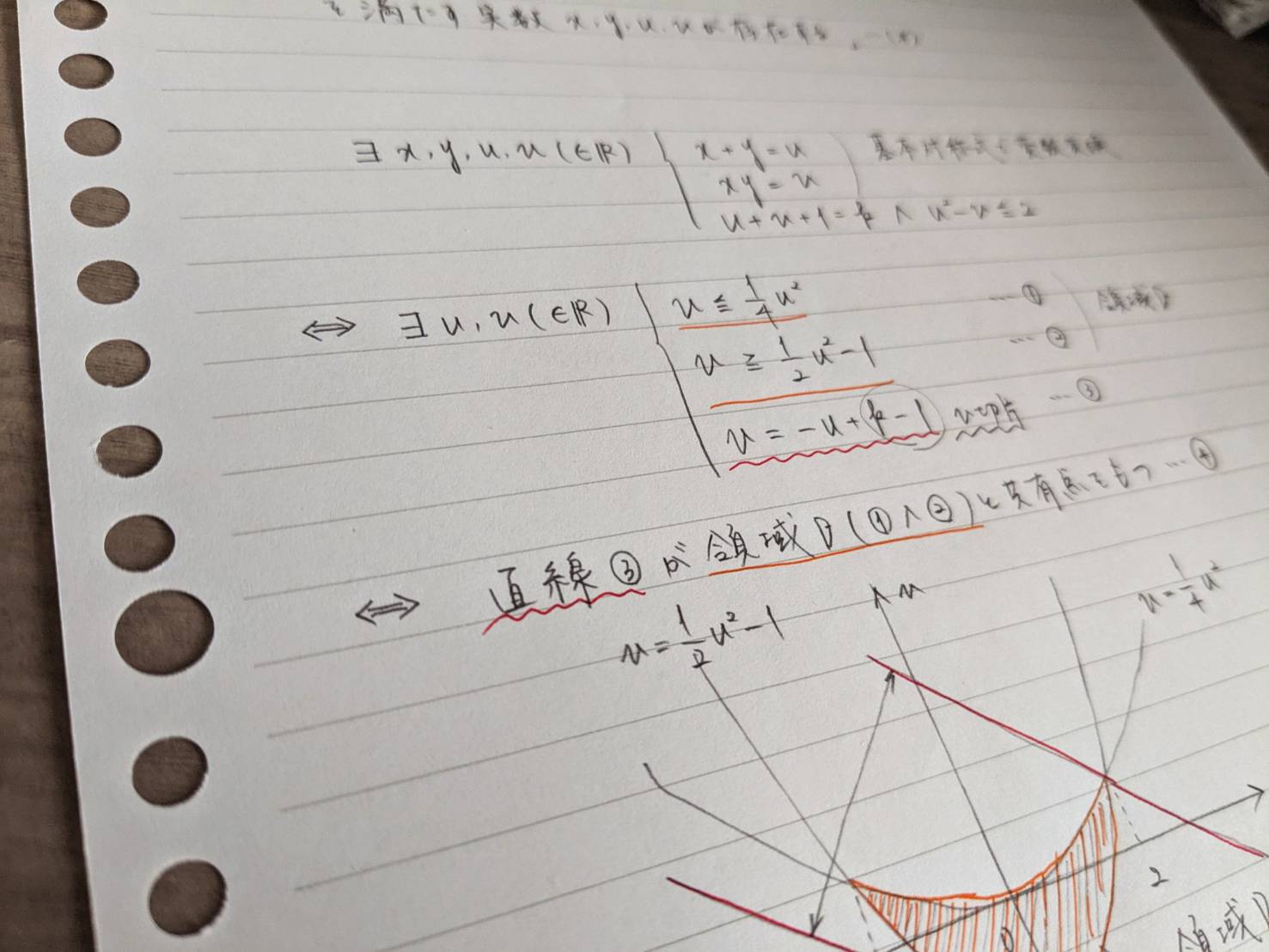
論理について学ぶと、数学全体への理解力が高まります。特に「図形と方程式」「最大・最小」「軌跡・領域」「ベクトル」といった分野で形式的な処理ができるようになり、標準的な問題ではもはや機械的作業のように感じられるようになります。また、変数の存在条件として値域を求めるといった高級な考え方や基本対称式で変数を変換したときの「実数条件」など、何となく分かるようで分かっていなかったことが納得できるようになるのではないでしょうか。
答案作成力の面でも大きなメリットがあります。模範解答の論理の構造や各作業の必然性を読めるようになることは、曖昧さのない答案を自分で作ることに役立ちます。また、最後まで計算できなかったとしても全体の方針を示しておくことで部分点を稼ぎ、得点力に繋がります。
このように、論理分野について固めておくことは答案作成をシステマチックなものにしたり、全体の骨組みを把握して点数に直結するような表現力・論証力を身につけるためには不可欠です。論理については難しく感じるかもしれませんが、逆にここが固まっていれば数学の勉強が楽になるのです。
著者の体験談
著者は浪人期の春休みから下記(4.)の映像講義や参考書を用いて論理を勉強しました。春にただ前年使ってた問題集を周回するのではなく、論理の分野の基礎を固めたという選択はかなり正しかったと思います。この勉強は間違いなく数学力の養成に役立っています。自分に足りていなかったのは、基礎のまた基礎の部分だったのだ、と実感することができました。予備校の講義の浸透力も段違いですし、問題集の模範解答も「読める!」と感じることが多くなりました。去年は「存在条件」とか全く分からずに見様見真似でやっていたものも明らかに使いこなすことができるようになったと思います。
実際に全体として数学力を高めることができ、およそ1年を通して共通テストの得点を数学1A2Bともに30~40点あげることができました。2次の記述型でも、模試で白紙が多かった現役時と比べて、圧倒的に部分点を稼ぐことができたと思います。入試前の過去問演習では、答案の添削が無くてもある程度正確な答案が書けるようになったと感じられました。
勉強方法について
教科書には一応「集合と論理」の単元はありますが、これだけではカバーしきれないため、より丁寧に教えてくれる専用の補助教材が必要です。今回は、導入としてのYouTube講義動画と、東進ブックスから出版されている参考書をご紹介します。動画を導入にして、参考書へと接続すればかなりの効果が期待できます。
YouTubeで分かりやすい講義動画が無料で提供されていますので、これらを活用しましょう。それほど時間はかからないため、まとまった時間で一気に視聴するとよいと思います。YouTubeの動画は下記のどちらかをおすすめします。
- Masaki Koga『同値を制する者、受験数学を制す』
- ガチでノビる受験数学 東大医学部の解説動画『論理攻略①+値域と軌跡(論理攻略②)』
- 青木純二『数学の真髄』(東進ブックス)
Masaki Koga『同値を制する者、受験数学を制す』
筆者も全編視聴しました。大変参考になるプレイリストです。軌跡の範囲は無いですが、導入としてエッセンスは十分です。自分で板書を移しつつ、最初の動画から順番に視聴していきましょう。
ガチでノビる受験数学 東大医学部の解説動画『論理攻略①+値域と軌跡(論理攻略②)』
こちらも本質的な講義動画がそろっているチャンネルです。他の分野の解説動画も受験生目線で作られていて参考になる点が多いです。
青木純二『数学の真髄』(東進ブックス)
上の動画からこの参考書へ接続してください。具体例が豊富で分かりやすいです。束や存在条件の考え方が非常に参考になりました。練習問題は余裕があればやりましょう。ちなみにベクトル編も最近出たそう。
参考書を読み終わったら
上記の動画や参考書や動画でインプットが終わったら、実際に問題演習をこなしていきましょう。学校で配られた問題集や、自分が使っている問題集の解説と上記の教材で自分が学んだことを照らし合わせながら勉強していきます。
・解法の整理 「存在命題」 「すべての~」、「任意の~」、「~がある」、「~が存在する」と言われたとき、どのようなアプローチをとる必要があるのか、整理しておきましょう。青チャート等の問題集によるものとは違う、異なった観点から問題が分類ができるはずです。
・頭の中で論理記号に翻訳しながら自分が使っている問題集の解説を読んでみましょう。今までよりも答案の構造・骨組みが理解できるのが実感できるはずです。
・別解が考えられるものはそれも試してみましょう。例えば通過領域を求める問題で、変数を固定して求める方法と、変数が存在する条件から求める方法の両方にアプローチしてみる、といった感じです。
まとめ
数学の勉強が「何が行われているのかよく分からないもの」を暗記する作業であり、それに苦しさを覚えている人に向けて記事を書いてみました。限界を感じて数学を捨ててしまう前に、上に述べたような勉強をしてみるのも決して無駄ではないでしょう。やる気は十分にあるのに何をしていいかが分からず、結果が出ないため、それが自分の努力量の問題だと自己否定してしまうのは勿体ないことだと思います。
数学を苦手とする人すべてが論理の勉強を通して各段に成績が上がるわけではないかもしれません。しかし、一部の人には「刺さる」勉強ができると思います。この勉強を通して、基礎の部分の大切さ、一つ一つ積み上げることの大切さを学べるのではないでしょうか。それは数学だけではなく、文系科目も含めた他の科目にも間違いなく通ずるものです。


コメント